« Code Gray » : différence entre les versions
(Page créée avec « Le code Gray ou code binaire réfléchi est une façon de coder les nombres entiers en binaire en faisant en sorte que, d'un nombre consécutif à un autre il n'y ai jamais qu'un seul bit modifié. {| class="wikitable" |+Exemple avec un mot de 4 bits !Nombre !Binaire !Code Gray |- |<code>0</code> |<code>0000</code> |<code>0000</code> |- |<code>1</code> |<code>0001</code> |<code>0001</code> |- |<code>2</code> |<code>0010</code> |<code>0011</code> |- |<code>3</code... ») |
m (→Mise en oeuvre) |
||
| (16 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
=== La théorie === | |||
Le code Gray ou code binaire réfléchi est une façon de coder les nombres entiers en binaire en faisant en sorte que, d'un nombre consécutif à un autre il n'y ai jamais qu'un seul bit modifié. | Le code Gray ou code binaire réfléchi est une façon de coder les nombres entiers en binaire en faisant en sorte que, d'un nombre consécutif à un autre il n'y ai jamais qu'un seul bit modifié. | ||
{| class="wikitable" | {| class="wikitable" | ||
|+Exemple avec un mot de 4 bits | |+Exemple avec un mot de 4 bits | ||
!Nombre | !Nombre | ||
!Hexa | |||
!Binaire | !Binaire | ||
!Code Gray | !Code Gray | ||
|- | |- | ||
|<code>0</code> | |||
|<code>0</code> | |<code>0</code> | ||
|<code>0000</code> | |<code>0000</code> | ||
|<code>0000</code> | |<code>0000</code> | ||
|- | |- | ||
|<code>1</code> | |||
|<code>1</code> | |<code>1</code> | ||
|<code>0001</code> | |<code>0001</code> | ||
|<code>0001</code> | |<code>0001</code> | ||
|- | |- | ||
|<code>2</code> | |||
|<code>2</code> | |<code>2</code> | ||
|<code>0010</code> | |<code>0010</code> | ||
|<code>0011</code> | |<code>0011</code> | ||
|- | |- | ||
|<code>3</code> | |||
|<code>3</code> | |<code>3</code> | ||
|<code>0011</code> | |<code>0011</code> | ||
|<code>0010</code> | |<code>0010</code> | ||
|- | |- | ||
|<code>4</code> | |||
|<code>4</code> | |<code>4</code> | ||
|<code>0100</code> | |<code>0100</code> | ||
|<code>0110</code> | |<code>0110</code> | ||
|- | |- | ||
|<code>5</code> | |||
|<code>5</code> | |<code>5</code> | ||
|<code>0101</code> | |<code>0101</code> | ||
| | |<code>0111</code> | ||
|- | |- | ||
|<code>6</code> | |||
|<code>6</code> | |<code>6</code> | ||
|<code>0110</code> | |<code>0110</code> | ||
| | |<code>0101</code> | ||
|- | |- | ||
|<code>7</code> | |||
|<code>7</code> | |<code>7</code> | ||
|<code>0111</code> | |<code>0111</code> | ||
| | |<code>0100</code> | ||
|- | |- | ||
|<code>8</code> | |||
|<code>8</code> | |<code>8</code> | ||
|<code>1000</code> | |<code>1000</code> | ||
| | |<code>1100</code> | ||
|- | |- | ||
|<code>9</code> | |||
|<code>9</code> | |<code>9</code> | ||
|<code>1001</code> | |<code>1001</code> | ||
| | |<code>1101</code> | ||
|- | |- | ||
|<code>10</code> | |<code>10</code> | ||
|<code>A</code> | |||
|<code>1010</code> | |<code>1010</code> | ||
| | |<code>1111</code> | ||
|- | |- | ||
|<code>11</code> | |<code>11</code> | ||
|<code>B</code> | |||
|<code>1011</code> | |<code>1011</code> | ||
| | |<code>1110</code> | ||
|- | |- | ||
|<code>12</code> | |<code>12</code> | ||
|<code>C</code> | |||
|<code>1100</code> | |<code>1100</code> | ||
| | |<code>1010</code> | ||
|- | |- | ||
|<code>13</code> | |<code>13</code> | ||
|<code>D</code> | |||
|<code>1101</code> | |<code>1101</code> | ||
| | |<code>1011</code> | ||
|- | |- | ||
|<code>14</code> | |<code>14</code> | ||
|<code>E</code> | |||
|<code>1110</code> | |<code>1110</code> | ||
| | |<code>1001</code> | ||
|- | |- | ||
|<code>15</code> | |<code>15</code> | ||
|<code>F</code> | |||
|<code>1111</code> | |<code>1111</code> | ||
| | |<code>1000</code> | ||
|} | |} | ||
Dernière subtilité quand on arrive "au bout" d'un mot binaire (ici 15) pour repasser à zéro on ne romps pas le truc, un passe de 15=<code>1000</code> à 0=<code>0000</code> donc encore un changement d'un seul bit! | |||
Quel est l'intérêt d'un tel code me direz vous ? | |||
Cela sert a faire des compteurs numériques de façon mécaniques par exemple. Imaginons que l'on ai un signal binaire qui s'excrément au fur et a mesure d'un process quelconque (on se limite à 3 bits pour coder en octal mais ce serait pareil avec plus) | |||
[[Fichier:Octal croissant.png|sans_cadre|440x440px]] | |||
Ici les 3 lignes (B<sub>0</sub>,B<sub>1</sub> et B<sub>3</sub>) sont '''parfaitement''' synchrones et qu'on lise le signe '''parfaitement''' au milieu de chaque état cela nous donne: | |||
Jusque là tout va bien. Imaginons que les lignes B<sub>0</sub>,B<sub>1</sub> et B<sub>3</sub> ne soient plus tout à fait en phase, ce qui peut arriver avec tout système mécanique. | |||
[[Fichier:Binaire déphase.png|sans_cadre|440x440px]] | |||
On voit bien que pas mal de lectures donnent de mauvaises valeurs car on se trouve dans un transition imparfaite. Le digit 6 par exemple B<sub>0</sub> est passé a zéro quand B<sub>1</sub> n'a pas encore changé. | |||
Comment pourrait on faire un système de décompte binaire qui sont insensible a ces problèmes? '''Avec le code binaire réfléchi ou code Gray!''' | |||
Si on change le signal binaire par un signal en code gray: | |||
[[Fichier:Code gray chronogrames.png|sans_cadre|440x440px]] | |||
On lit la valeur au début: | |||
Ok on commence à zéro. La "ruse" est qu'il suffit d'attendre que l'un des bits changes de valeur, sachant que jamais deux ne peuvent changer en même temps. | |||
Premier changement c'est la ligne B<sub>0</sub> et on lit <code>001</code> qui en code gray donne 1. Après 0 on a bien un 1. Jusqu'ici tout va bien! | |||
On attends le prochain changement : | |||
La ligne B<sub>1</sub> a changé et on a donc <code>011</code> qui code un 2 en gray. Apres 1 on a bien 2.... on continue: | |||
Ensuite B<sub>0</sub> repasse à zéro donc <code>010</code> qui code un 3. | |||
Par la suite B<sub>2</sub> passe à un <code>100</code> code un 4 ... bien après le 3 c'est un 4. | |||
Et ca marche! | |||
On remarque également que la fréquence du signal du bit "B<sub>0</sub>" est divisé par deux en code Gray. On a donc besoin d'un support physique de moins bonne qualité (ou on peut augmenter le débit de 100%) en code binaire réfléchi qu'en binaire simple. | |||
'''Tout ceci est valable pour coder des valeurs croissantes ou décroissantes. Pour toute autre suite cela n'aura aucun sens.''' | |||
=== Mise en oeuvre === | |||
On peut réaliser une roue codeuse en code GRAY: | |||
[[Fichier:Encoder Disc (3-Bit).svg.png|sans_cadre]] | |||
Si on la lit avec 3 photodiodes on a un encodeur d'angle précis à 45°. Et c'est la même méthode, on attends qu'un bit change pour lire la nouvelle valeur. | |||
J'ai même trouvé: | |||
[[Fichier:Gray code precis.gif|sans_cadre]] | |||
J'ai compté 10 bits donc mieux que 0,35° de précision. | |||
Merci à http://m.joffroy.free.fr/in/Cours%20BTS%20MAI%201er%20et%202eme%20ann%C3%A9e/COURS%2009%20Les%20capteurs/Codeur%20Absolu.htm | |||
=== Implémentation === | |||
On voit que le code Gray n'a que des avantages. En revanche il semble un peut complexe à coder / décoder. En fait non et démonstration ci-dessous. | |||
==== Codage/décodage hardware ==== | |||
L'opérateur booléen utilisé est le "ou exclusif" noté ⨁. | |||
===== Codage (binaire vers Gray) ===== | |||
On considère le bit de poids n. G<sub>n</sub> est la valeur du bit en code Gray et B<sub>n</sub> la valeur en code binaire. | |||
G<sub>n</sub>=B<sub>n</sub> ⨁ B<sub>(n+1)</sub>. | |||
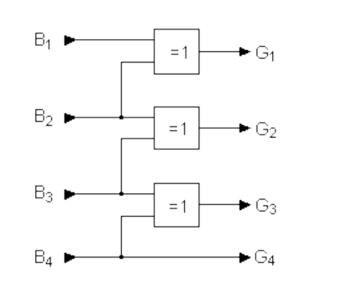
Si on veut coder 8 bits on utilise le schéma : | |||
[[Fichier:Codage gray.png|sans_cadre|343x343px]] | |||
===== Décodage (Gray vers binaire) ===== | |||
La formule est : | |||
B<sub>n</sub>=G<sub>n</sub> ⨁ B<sub>(n+1)</sub> | |||
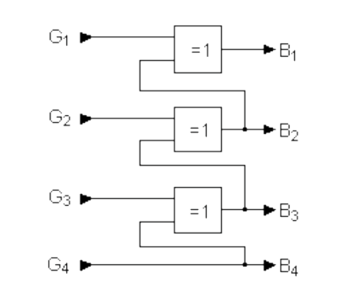
Le schéma donne : | |||
[[Fichier:Conversion gray vers binaire.png|sans_cadre|344x344px]] | |||
On peut trouver là un super convertisseur en ligne sur 4 bits | |||
https://ressources.univ-lemans.fr/AccesLibre/UM/Pedago/physique/02/electro/codegray.html | |||
==== Exemple de code "C" ==== | |||
On va utilisera du code en "C".<syntaxhighlight lang="c"> | |||
typedef unsigned int uint; | |||
// Cette fonction reprends le schéma ci-dessus | |||
uint BinaryToGray(uint num) | |||
{ | |||
return num ^ (num >> 1); // L'operateur >> est un décalage binaire vers la droite. ^ est un ou exclusif. | |||
} | |||
// Toujours selon le schéma ci-dessus. | |||
uint GrayToBinary(uint num) | |||
{ | |||
uint mask = num; | |||
while (mask) { | |||
mask >>= 1; | |||
num ^= mask; | |||
} | |||
return num; | |||
} | |||
// plus performant mais pour 32 bits. On peut l'adapter... | |||
uint GrayToBinary32(uint num) | |||
{ | |||
num ^= num >> 16; | |||
num ^= num >> 8; | |||
num ^= num >> 4; | |||
num ^= num >> 2; | |||
num ^= num >> 1; | |||
return num; | |||
} | |||
</syntaxhighlight> | |||
Version actuelle datée du 24 novembre 2025 à 21:13
La théorie
Le code Gray ou code binaire réfléchi est une façon de coder les nombres entiers en binaire en faisant en sorte que, d'un nombre consécutif à un autre il n'y ai jamais qu'un seul bit modifié.
| Nombre | Hexa | Binaire | Code Gray |
|---|---|---|---|
0
|
0
|
0000
|
0000
|
1
|
1
|
0001
|
0001
|
2
|
2
|
0010
|
0011
|
3
|
3
|
0011
|
0010
|
4
|
4
|
0100
|
0110
|
5
|
5
|
0101
|
0111
|
6
|
6
|
0110
|
0101
|
7
|
7
|
0111
|
0100
|
8
|
8
|
1000
|
1100
|
9
|
9
|
1001
|
1101
|
10
|
A
|
1010
|
1111
|
11
|
B
|
1011
|
1110
|
12
|
C
|
1100
|
1010
|
13
|
D
|
1101
|
1011
|
14
|
E
|
1110
|
1001
|
15
|
F
|
1111
|
1000
|
Dernière subtilité quand on arrive "au bout" d'un mot binaire (ici 15) pour repasser à zéro on ne romps pas le truc, un passe de 15=1000 à 0=0000 donc encore un changement d'un seul bit!
Quel est l'intérêt d'un tel code me direz vous ?
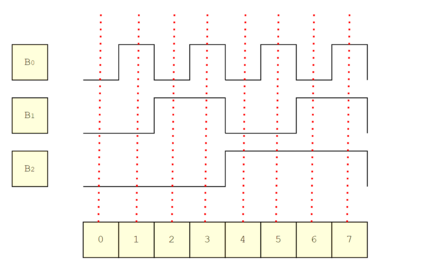
Cela sert a faire des compteurs numériques de façon mécaniques par exemple. Imaginons que l'on ai un signal binaire qui s'excrément au fur et a mesure d'un process quelconque (on se limite à 3 bits pour coder en octal mais ce serait pareil avec plus)
Ici les 3 lignes (B0,B1 et B3) sont parfaitement synchrones et qu'on lise le signe parfaitement au milieu de chaque état cela nous donne:
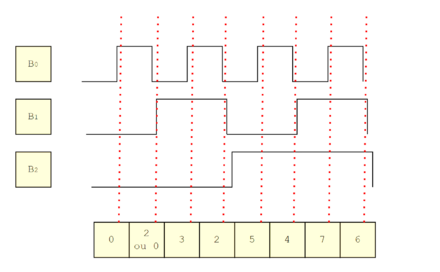
Jusque là tout va bien. Imaginons que les lignes B0,B1 et B3 ne soient plus tout à fait en phase, ce qui peut arriver avec tout système mécanique.
On voit bien que pas mal de lectures donnent de mauvaises valeurs car on se trouve dans un transition imparfaite. Le digit 6 par exemple B0 est passé a zéro quand B1 n'a pas encore changé.
Comment pourrait on faire un système de décompte binaire qui sont insensible a ces problèmes? Avec le code binaire réfléchi ou code Gray!
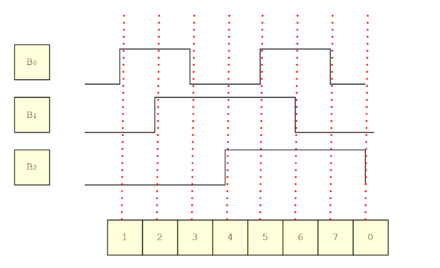
Si on change le signal binaire par un signal en code gray:
On lit la valeur au début:
Ok on commence à zéro. La "ruse" est qu'il suffit d'attendre que l'un des bits changes de valeur, sachant que jamais deux ne peuvent changer en même temps.
Premier changement c'est la ligne B0 et on lit 001 qui en code gray donne 1. Après 0 on a bien un 1. Jusqu'ici tout va bien!
On attends le prochain changement :
La ligne B1 a changé et on a donc 011 qui code un 2 en gray. Apres 1 on a bien 2.... on continue:
Ensuite B0 repasse à zéro donc 010 qui code un 3.
Par la suite B2 passe à un 100 code un 4 ... bien après le 3 c'est un 4.
Et ca marche!
On remarque également que la fréquence du signal du bit "B0" est divisé par deux en code Gray. On a donc besoin d'un support physique de moins bonne qualité (ou on peut augmenter le débit de 100%) en code binaire réfléchi qu'en binaire simple.
Tout ceci est valable pour coder des valeurs croissantes ou décroissantes. Pour toute autre suite cela n'aura aucun sens.
Mise en oeuvre
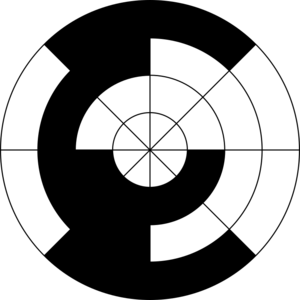
On peut réaliser une roue codeuse en code GRAY:
Si on la lit avec 3 photodiodes on a un encodeur d'angle précis à 45°. Et c'est la même méthode, on attends qu'un bit change pour lire la nouvelle valeur.
J'ai même trouvé:
J'ai compté 10 bits donc mieux que 0,35° de précision.
Implémentation
On voit que le code Gray n'a que des avantages. En revanche il semble un peut complexe à coder / décoder. En fait non et démonstration ci-dessous.
Codage/décodage hardware
L'opérateur booléen utilisé est le "ou exclusif" noté ⨁.
Codage (binaire vers Gray)
On considère le bit de poids n. Gn est la valeur du bit en code Gray et Bn la valeur en code binaire.
Gn=Bn ⨁ B(n+1).
Si on veut coder 8 bits on utilise le schéma :
Décodage (Gray vers binaire)
La formule est :
Bn=Gn ⨁ B(n+1)
Le schéma donne :
On peut trouver là un super convertisseur en ligne sur 4 bits
https://ressources.univ-lemans.fr/AccesLibre/UM/Pedago/physique/02/electro/codegray.html
Exemple de code "C"
On va utilisera du code en "C".
typedef unsigned int uint;
// Cette fonction reprends le schéma ci-dessus
uint BinaryToGray(uint num)
{
return num ^ (num >> 1); // L'operateur >> est un décalage binaire vers la droite. ^ est un ou exclusif.
}
// Toujours selon le schéma ci-dessus.
uint GrayToBinary(uint num)
{
uint mask = num;
while (mask) {
mask >>= 1;
num ^= mask;
}
return num;
}
// plus performant mais pour 32 bits. On peut l'adapter...
uint GrayToBinary32(uint num)
{
num ^= num >> 16;
num ^= num >> 8;
num ^= num >> 4;
num ^= num >> 2;
num ^= num >> 1;
return num;
}