« Code Gray » : différence entre les versions
mAucun résumé des modifications |
mAucun résumé des modifications |
||
| Ligne 96 : | Ligne 96 : | ||
[[Fichier:Signal Binaire 4 bits a lecture synchrone.png|sans_cadre]] | [[Fichier:Signal Binaire 4 bits a lecture synchrone.png|sans_cadre]] | ||
Jusque là tout va bien. Imaginons que les lignes A,B,C et B ne soient pas bien en phase. | |||
[[Fichier:Signal asynchones.png|sans_cadre]] | |||
On voit bien que le 7 qui doit être <code>0100</code> est <code>11xx</code> avec <code>x</code> où sait pas bien si c'est un 0 ou un 1. | |||
Comment pourrait on faire un système de décompte binaire qui sont insensible a ces problèmes? '''Avec le code binaire réfléchi ou code Gray!''' | |||
Si on change le signal binaire par un signal en code gray: | |||
[[Fichier:Gray code.png|sans_cadre]] | |||
On lit la valeur au début: | |||
[[Fichier:0 en binaire reflechi.png|sans_cadre]] | |||
Ok on commence à zéro. La "ruse" est qu'il suffit d'attendre que l'un des bits changes de valeur, sachant que jamais deux ne peuvent changer en même temps. | |||
[[Fichier:Gray à 1.png|sans_cadre]] | |||
Premier changement c'est la ligne D et on lit <code>0001</code> qui en code gray donne 1 . Après 0 on a bien un 1. Jusqu'ici tout va bien! | |||
On attends le prochain changement : | |||
[[Fichier:Gray 2.png|sans_cadre]] | |||
La ligne C a changé et on a donc 0011 qui code un 2 en gray. Apres 1 on a bien 2.... on continue: | |||
[[Fichier:Gray.png|sans_cadre]] | |||
Et ca marche! | |||
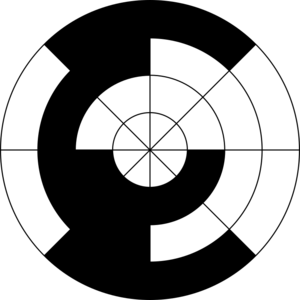
On peut également penser à une roue codeuse en code GRAY: | |||
[[Fichier:Encoder Disc (3-Bit).svg.png|sans_cadre]] | |||
Si on la lit avec 3 photodiodes on a un encodeur d'angle précis à 45°. Et c'est la même méthode, on attends qu'un bit change pour lire la nouvelle valeur. | |||
Version du 20 mars 2025 à 16:20
Le code Gray ou code binaire réfléchi est une façon de coder les nombres entiers en binaire en faisant en sorte que, d'un nombre consécutif à un autre il n'y ai jamais qu'un seul bit modifié.
| Nombre | Hexa | Binaire | Code Gray |
|---|---|---|---|
0
|
0
|
0000
|
0000
|
1
|
1
|
0001
|
0001
|
2
|
2
|
0010
|
0011
|
3
|
3
|
0011
|
0010
|
4
|
4
|
0100
|
0110
|
5
|
5
|
0101
|
0111
|
6
|
6
|
0110
|
0101
|
7
|
7
|
0111
|
0100
|
8
|
8
|
1000
|
1100
|
9
|
9
|
1001
|
1101
|
10
|
A
|
1010
|
1111
|
11
|
B
|
1011
|
1110
|
12
|
C
|
1100
|
1010
|
13
|
D
|
1101
|
1011
|
14
|
E
|
1110
|
1001
|
15
|
F
|
1111
|
1000
|
Quel est l'intérêt d'un tel code me direz vous ?
Cela sert a faire des compteurs numériques de façon mécaniques par exemple. Imaginons que l'on ai un signal binaire qui s'excrément au fur et a mesure d'un process quelconque.
Fichier:Signal Binaire 4 bits.png
Si les 4 lignes (A,B,D et D) sont parfaitement synchrones et qu'on lise le signe parfaitement au milieu de chaque état cela nous donne:
Fichier:Signal Binaire 4 bits a lecture synchrone.png
Jusque là tout va bien. Imaginons que les lignes A,B,C et B ne soient pas bien en phase.
On voit bien que le 7 qui doit être 0100 est 11xx avec x où sait pas bien si c'est un 0 ou un 1.
Comment pourrait on faire un système de décompte binaire qui sont insensible a ces problèmes? Avec le code binaire réfléchi ou code Gray!
Si on change le signal binaire par un signal en code gray:
On lit la valeur au début:
Fichier:0 en binaire reflechi.png
Ok on commence à zéro. La "ruse" est qu'il suffit d'attendre que l'un des bits changes de valeur, sachant que jamais deux ne peuvent changer en même temps.
Premier changement c'est la ligne D et on lit 0001 qui en code gray donne 1 . Après 0 on a bien un 1. Jusqu'ici tout va bien!
On attends le prochain changement :
La ligne C a changé et on a donc 0011 qui code un 2 en gray. Apres 1 on a bien 2.... on continue:
Et ca marche!
On peut également penser à une roue codeuse en code GRAY:
Si on la lit avec 3 photodiodes on a un encodeur d'angle précis à 45°. Et c'est la même méthode, on attends qu'un bit change pour lire la nouvelle valeur.