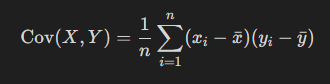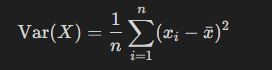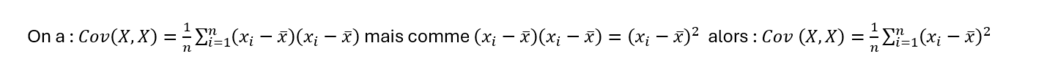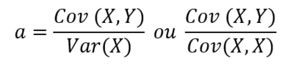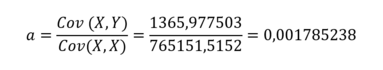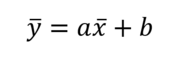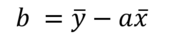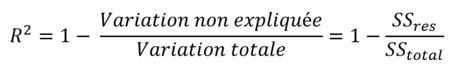Louise

Page pour expliquer les statistiques de base à Louise

Dans cet article il y a des encarts. En voici la légende.

Légende des encarts

	C'est une info en plus qui me semble explique le pourquoi. Si ca aide pas on l'oublie
	Signale un "point dur" il faut le comprendre pour passer à la suite.

Les données.

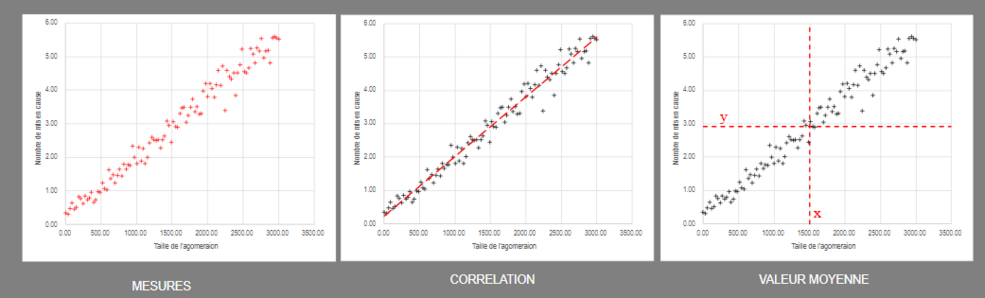
On dispose de données mesurées (données quantitatives discrètes)

On mesure le nombre de mises en causes par la police en fonction de la taille de l'agglomération (la variable explicative)

Exemple de valeurs

Taille Agglo	Nb Mise en cause
0.00	0.33
30.30	0.30
60.61	0.46
90.91	0.64
121.21	0.45
151.52	0.50
181.82	0.83
212.12	0.76
242.42	0.62
272.73	0.84
303.03	0.73
333.33	0.78
363.64	0.95
393.94	0.64
424.24	0.73
454.55	0.98
....	....

On voit intuitivement que le loi qui régie le phénomène observé semble être une droite. Comment confirmer cela. On peut d'abord demander à Excel 😊

Il y a une fonction dans Excel pour faire cela. Il est même capable de calculer l'équation de la droite (y=ax+b avec a=0.0018 et b=0,2309). Il nous donne bien entendu la valeur de R².

Mais c'est trop facile calculons le nous même

Rappels de mathématiques

On va avoir besoin de quelques concepts mathématiques pour nos calculs à venir. Je les détaille dans cette section avec leurs convention d'écriture.

Le concept d'écart

Dans la suite on va utiliser le concept d'écart d'une valeur par rapport à une valeur de référence. Dans notre cas on a 3 types de valeurs.

1. Les mesures. Ce sont les valeurs que l'on se propose d'étudier (ici le nombre de mis a cause en fonction de la taille de l'agglomération)
2. La corrélation : C'est la loi qui nous semble exprimer le mieux la répartition de nos valeurs. (Ici c'est une droite mais, dans des cas plus complexe on pourait penser à une autre courbe).
3. Les moyennes : On peut utiliser des valeurs statistiques diverses comme ici la moyenne. La moyenne de X correspond à la taille moyenne des agglomérations dans notre étude. La moyenne Y correspond au nombre moyen de mises en causes quelle que soit l'agglomération.

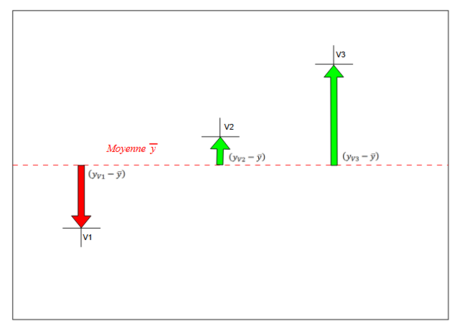
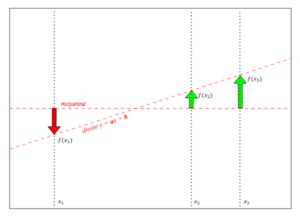
Dans la suite on va parler des écarts d'une valeur par rapport à une autre. Par exemple l'écart des laveurs de l'étude par rapport à la moyenne.

Attention

Pour la suite, je prends un exemple avec seulement 3 points paracerque ça me saoule de faire les dessins pour les 1000 points des graphiques vus plus haut mais normalement on fait les calculs pour TOUS les ponts de la série

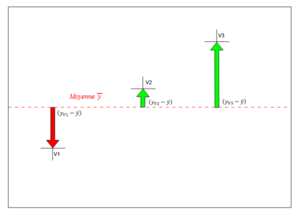
Dans cet exemple on a trois valeurs V1, V2 et V3 les trois écarts sont indiqués pas des flèches (rouge c'est négatif et vert c'est positif).

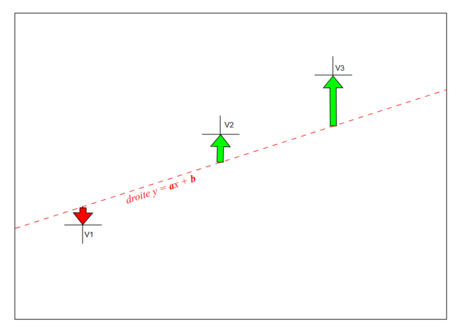
Ici mon mesure l'écart entre la valeur que l'on a mesurer par rapport à la valeur donnée par notre droite y=ax+b (la loi qui nos semble donner une meilleure idée de ce que nous observons).

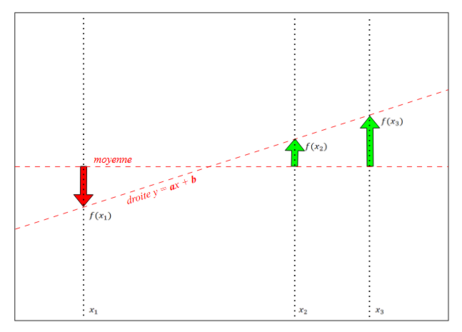
Le dernier écart que nous pourrions avoir a mesurer c'est celu entre la valeur issue de y=ax+b et la moyenne.

On a toujours un écart entre la moyenne et le résultat de la fonction y=ax+b pour x=x₁.

Le concept de somme

Dans la suite du cours on aura souvent des sommes d'écarts.

Cette somme est notée avec la lettre Sigma Σ(...) qui signifie la somme de tous les éléments donnés dans la parenthèse.

Dans le cas du dessus avec un écart entre f(x) et la moyenne de y on écrira : 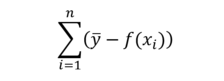En dessous du Σ on a la variable qui sera utilisée dans la parenthèse (i) et qui variera de 1 (i=1) à n (le n au dessus du Σ) Dans notre cas ci dessus on à 3 mesures et donc : 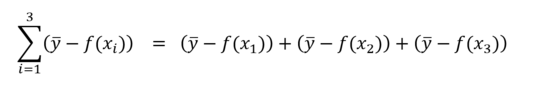C'est la somme des trois flèches du graphique ci dessus. Pour les données complètes (les 1000 valeurs) on aurait :

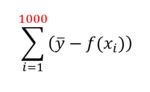
Bon nous avons les bases on peut reprendre le calcul de la droite de corrélation.

Calcul de la droite f(x)=y=ax+b

f est la fonction qui pour une valeur de x (taille de l'agglo) donne la valeur estimée par notre intuition qu'une droite explique le phénomène observé. On note la valeur pour un x donné f(x).

Remarque

f(x) représente n'importe quelle fonction. Ici on a dit que f(x)=ax + b mais on aurait pu avoir f(x)=x² ou même f(x)=sin(2x)+cos(-2x). f(x) c'est une notation abstraite pour un "truc" qui transforme un nombre x pour donner un autre nombre y (ou f(x).

Par définition on sait que :

La pente de la droite a correspond au rapport entre le covariance des deux variables et la variance de la variable explicative (x)

La formule de la covariance est :

Donc c'est la somme (Σ) du:

la multiplication entre l'écart entre une valeur de x et la moyenne des x (x avec une barre dessus) et l'écart entre y et sa mpyenne.

Le tout divisé par le nombre de mesures n.

Les calculatrices savent, en général, faire ce calcul.

On remarque que c'est la même formule que si on calculait la covariance de la variable x avec elle même:

Calcul de a

Donc, d'après la définition le coefficient a:

Si on calcule a pour nos 1000 valeurs données ci dessus :

On avait vu qu'Excel avait trouvé 0,0018 au début du chapitre. On est encore plus précis que Excel mais on trouve la même valeur.

Calcul de b

On dit dans le cours que b est la valeur de y pour x=0 c'est bien beau mais on le calcule comment? Je sais pas si c'est au programme mais c'est pas plus compliqué que pour a. C'est même hyper simple.

Il faut simplement calculer la moyenne de x (moyenne des tailles d'agglo) et la moyenne de y (le nombre moyen de mis en cause).

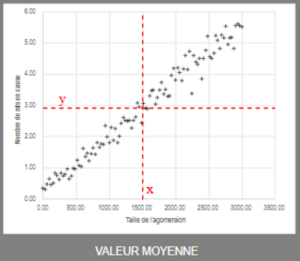
Si on regarde la valeur moyenne sur le schéma:

Pour le point a l'intersection entre la moyenne de x et celle de y on a un point. On considère que la droite va passer par ce point (ça doit se démontrer mais c'est pas je sujet ici) donc la valeur de la moyenne de y va dépendre de la valeur de la moyenne de x avec :

Donc :

Avec les valeurs correspondant à nos mesures :

On trouve 0,230911135 quand Excel avait trouvé 0,2309. On est encore meilleur que Excel!

Calcul du coefficient de détermination R².

A ce niveau de notre étude on à :

• 1000 mesures de nombre de mise en causes par rapport la la population de l'agglo
• Une représentation graphique sur laquelle il nous semble bien que nous avons a faire à une droite. On fait donc l'hypothèse que notre phénomène réponds a une loi linéaire.
• Le calcul des coefficients a et b de la droite passant au plus près de nos valeurs.

Maintenant on voudrais avoir une idée de la justesse de notre hypothèse. Est-elle bonne ou pas?

On calcule alors un coefficient de détermination R² dont la valeur est entre 0 et 1

Remarque

En math on note : R² Є [0...1] donc R² appartient à l'ensemble des nombres 0 et 1.

• 0 : C'est qu'on s'est complètement trompé. Nos valeurs ne répondent pas du tout a une loi linéaire.
• 1 : C'est parfait tous nos points sont su la droite.

Il est très rare que l'on soit a 0 ou 1 en général on a un chiifre qui s'approche de 1 car on a quand même vu que nos points ressemblaient bien à une droite.

La formule du cours reste assez vague sur la notion de Variation non expliquée et de variation totale.

La variation non expliquée représente l'écart entre la valeur de notre droite par rapport à la moyenne.

C'est ce que l'on a vu plus haut :

La variation totale représente l'écart entre la valeur mesurée (issue de notre enquête) et la moyenne.

On avait aussi vu cet écart plus haut:

Dans les deux cas on s'intéresse à la distance du point de la référence. Qu'elle soit positive ou négative on s'en fiche. Pour ça on prends le carré.

Attention

Encore une notation mathématique qui apparait ici! ŷ signifie le y calculé avec y=ax+b dans notre cas. Je l'ai aussi symbolisé f(x). Donc : ŷ = ax+b = f(x) ce sont trois façon d'écrire le résultat de l'équation de notre droite.

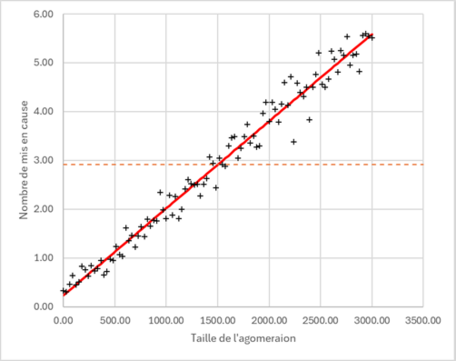
Donc on a les points issue de notre étude (les croix noires) et la courbe qu'on viens de calculer (la ligne rouge) et la moyenne des y (en orange pointillé)

SS_res c'est la somme des carrés des distances entre une croix et le point sur la ligne rouge correspondant au même x.

SS_tot c'est la somme des carrés des distances entre la ligne rouge et la valeur de la moyenne (la ligne orange) pour un x donné.

R² cest 1 - la division des deux valeurs ci dessus.

On remarque que l'on travaille partout avec des sommes de carrés donc à la fin c'est normal qu'on ait un carré R². De même le 1 est aussi un carré car 1²=1x1=1!

Si on fait le calcul on trouve R²=0.975983101 et excel avait trouvé 0,976. Encore une fois on est plus précis que Excel!